Missile Performance
The missile performance equations were taken from a http://www.dbf.gatech.edu/performance.ppt The equations estimate the missile's normal force and parasite drag (tangential force) coefficients. The coefficients have been non-dimensionalized with respect to the reference area based on the missile diameter.Parasite Drag Coefficient
![$ CD_{0, body, wave} = \left( 1.59 + \frac{1.83}{M^2} \right) \left\{ tan^{-1} \left[ \frac{0.5}{\left( \frac{l_N}{d} \right)} \right] \right\}^{1.69} $](form_0.png) for M > 1,
for M > 1, 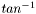 in rad
in rad
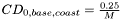 if M > 1, and
if M > 1, and
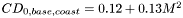 if M < 1
if M < 1
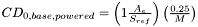 if M > 1, and
if M > 1, and
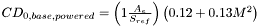 if M < 1
if M < 1
![$ CD_{0, body, friction} = 0.053 \left( \frac{l}{d} \right) \left[ \frac{M}{ql} \right]^{0.2} $](form_6.png) q in psf, l in ft.
q in psf, l in ft.
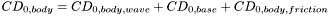
Note: 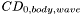 = body zero-lift wave drag coefficient,
= body zero-lift wave drag coefficient, 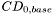 = body base drag coefficient,
= body base drag coefficient, 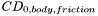 = body skin friction drag coefficient,
= body skin friction drag coefficient, 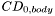 = body zero-lift drag coefficient,
= body zero-lift drag coefficient, 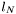 = nose length, d = missile diameter, l = missile body length,
= nose length, d = missile diameter, l = missile body length, 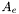 = nozzle exit area,
= nozzle exit area, 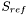 = reference area, q = dynamic pressure
= reference area, q = dynamic pressure
![$ CD_{0, wing, friction} = n_W \left\{ 0.0133 \left[ \frac{M}{q c_{mac}} \right]^{0.2} \right\} \left( \frac{2 S_{wet}}{S_{ref}} \right) $](form_15.png) q in psf, cmac in ft
q in psf, cmac in ft
![$ CD_{0, wing, wave} = n_W \left[ \frac{2}{\gamma M_{LE}^2} \right] \left\{ \left\{ \frac{( \gamma + 1 ) M_{LE}^2 }{2} \right\} ^{\frac{\gamma}{\gamma - 1}} \left\{\frac{\gamma + 1}{2 \gamma M_{LE}^2 – (\gamma - 1)}\right\}^{\frac{1}{\gamma - 1}} – 1 \right\} sin^2 \delta_{LE} cos \Delta_{LE} t_{mac} \frac{b}{S_{ref}} $](form_16.png) based on Newtonian impact theory.
based on Newtonian impact theory.
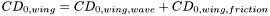
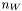 = number of wings ( cruciform = 2 ), q = dynamic pressure in psf,
= number of wings ( cruciform = 2 ), q = dynamic pressure in psf, 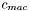 = length of mean aero chord in ft,
= length of mean aero chord in ft, 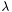 = Specific heat ratio = 1.4,
= Specific heat ratio = 1.4, 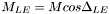 = Mach number perpendicular to the leading edge,
= Mach number perpendicular to the leading edge, 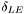 = leading edge section total angle,
= leading edge section total angle, 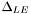 = leading edge sweep angle,
= leading edge sweep angle, 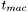 = max thickness at mean aerodynamic chord, b = span
= max thickness at mean aerodynamic chord, b = span
Normal Force Coefficient
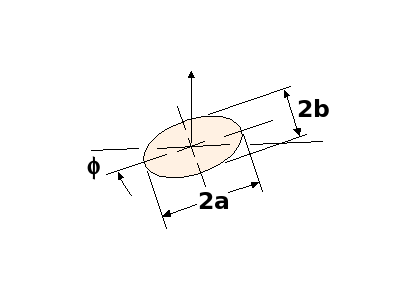
![$ |C_{N, body}| = \left[|\frac{a}{b} cos \phi + \frac{b}{a} sin \phi |\right] \left[| sin ( 2\alpha ) cos ( \frac{\alpha}{2} ) | + 2 \frac{l}{d} sin^2 \alpha \right] $](form_25.png)
![$ |C_{N, wing}| = \left[ \frac{4|sin \alpha’ cos \alpha’|}{(M^2 – 1)^{\frac{1}{2}}} + 2 sin^2 \alpha’ \right] \left( \frac{S_w}{S_{ref}} \right) $](form_26.png) , if
, if ![$ M > \left\{ 1 + \left[ \frac{8}{ \pi A } \right]^2 \right\}^{\frac{1}{2}} $](form_27.png)
![$ |C_{N, wing}| = \left[ \frac{\pi A}{2}|sin \alpha’ cos \alpha’| + 2 sin^2 \alpha’ \right] \left( \frac{S_w}{S_{ref}} \right) $](form_28.png) , if
, if ![$ M < \left\{ 1 + \left[ \frac{8}{ \pi A } \right]^2 \right\}^{\frac{1}{2}} $](form_29.png)
Note: Linear wing theory applicable if ![$ M > \left\{ 1 + \left[ \frac{8}{ \pi A } \right]^2 \right\}^{\frac{1}{2}} $](form_27.png) , slender wing theory applicable if
, slender wing theory applicable if ![$ M < \left\{ 1 + \left[ \frac{8}{ \pi A } \right]^2 \right\}^{\frac{1}{2}} $](form_29.png) , A = Aspect Ratio,
, A = Aspect Ratio, 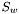 = Wing Planform Area,
= Wing Planform Area, 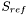 = Reference Area
= Reference Area
 1.5.5
1.5.5